Tag Archives: social networks

One Love: the missing paper on the network of romantic partnership in polyamory

2 Replies

Is polyamory a single, global web of love?

Polyamory is a relationship style where people engage in multiple, committed, romantic relationships at the same time. In the West, more and more people who practice it have been coming together in communities arranged roughly by country. A good resource for people who want to know more is Franklin Veaux’s website.

In this post, I do not talk about polyamory per se. Rather, I want to remark on the insights you can get if you think about it as a social network. Each polyamorous person is a node in the network. Nodes are connected by edges, encoding the romantic relationships across people. Now, in 1959, Paul Erdös and Alfred Rényi wrote a famous graph theory paper. Among other results, they proved that:

  • If you take a network consisting of a number of disconnected nodes;
  • And then start adding one link at a time, each edge connecting any two nodes picked at random, then;
  • When the number of links of the average node exceeds 1, a giant component emerges in the network. In a network, a component is a group of nodes that are all reachable from each other, directly or indirectly. A giant component is a component that consists of a large proportion of all nodes in the network. If a network has a giant component, most of its nodes are reachable from most other nodes.

Almost by definition the average polyamorists has more than one relationship. Granted, some people will only have one: maybe they are monogamous partners of a polyamorous person, or maybe they are still building their own constellation. Ther are even people who identify as polyamorous but are currently single. But there is also quite a high proportion of people with two or more partners. So, under most real-world conditions, the number of partners of the average person in the polyamory community is greater than one.

So, we have a mathematical theorem about random graphs and an educated guess about polyamory. When we put the two together, we obtain a sweeping hypothesis: most polyamorists in the world are connected to each other by a single web of love. Everyone is everyone else’s lover’s lover’s lover’s lover – six degrees of separation, but in romance. This would be an impressive macrostructure in society. Is it really there? There is a missing paper here. How to disprove the hypothesis and write it?

A statistical physics-ish approach

The hypothesis is quite precise, and in principle testable. But there are are substantial practical difficulties. You’d need unique identifiers for every poly person in the world, to make sure that Alice, Bob’s lover, is not the same person as Alice, Chris’s lover. Some people perceive a stigma around polyamory, and even many of those who don’t prefer to keep their relationship choices to themselves. So, the issues around research ethics, privacy and data protection are formidable.

So, maybe we can take a page out of the statistical physics playbook. The idea  of statistical physics is to infer a property of the whole system (in this case, the property is the existence of a giant component in the polyamory network) from statistical, rather than deterministic, information on the system’s components (in this case, the average number of partners per person). In our case, you could:

  1. Build computer simulations of polyamorous networks, and see if, for a realistic set of assumption, there is a value of the average number of relationships R that triggers a phase transition where a giant component emerges in the network.
  2. Run a simple survey (anonymous, sidestepping the ethics/privacy/data protection problems) to ask polyamorists how many relationship they have. Try also to validate assumptions underpinning your simulations.
  3. Compare the average number of relationships R’ as it results from the survey with the trigger value R as it results from the simulation. If R’>R, then most polyamorists are indeed connected to each other by a single web of love.

In the rest of this post, I am going to think aloud around step 1. At the very end I add a few considerations on step 2.

The model

Models are supposed to be abstract, not realistic. But the assumptions behind the Erdös-Rényi random graph model (start with disconnected nodes, add edges at random) are a bit too unrealistic for our case. I tried to build my own model starting from a different set of assumptions:

  • I assume that, as is often the case in real life, people move into polyamory by opening their previously monogamous relationships. So, I start from a set of couples, not of individuals. In network terms, this means starting with a network with N nodes, organized into N/2 separate components with 2 nodes each. N/2 is also the number of edges in the initial network.
  • At every time step, I add an edge between two random individuals that are not already connected. We ignore gender, and assume any person can fall in love with any other person.

Notice that, at time 0, all nodes of the network have one incident edge. In an Erdös-Rényi graph, we would already see a giant component, but this is not an Erdös-Rényi graph. In fact, we can think of it in a different way: we can redefine nodes as couples, rather than individuals. This way, we obtain a completely disconnected network with N/2 node. As we add edges in the original network of individuals, we now connect couples; and we are back into the Erdös-Rényi model, except with N/2 couples instead of N individuals. By the 1959 result, a giant component connecting most couples emerges when the average couple has over one incident edge: in other words, when there are N/4 inter-couple edges (since one edge always connects two couples, or, more precisely, two people in two different couples).

How many edges do individual people have on average at this point? There were N/2 intra-couple edges at the beginning; we then added N/4 inter-couple new ones. This means our network has now N x 3/4 edges. Each edge is incident to two individuals; so, the average individual has 1.5 incident edges.

Let us restate our result in polyamory terms.

Start from a number of monogamous couples. At each time period, add a new romantic relationship between two randomly chosen individuals that are not already in a relationship with each other. When the average number of relationships exceeds 1.5, a large share of individuals are connected to each other by an unbroken path of romantic relationships.

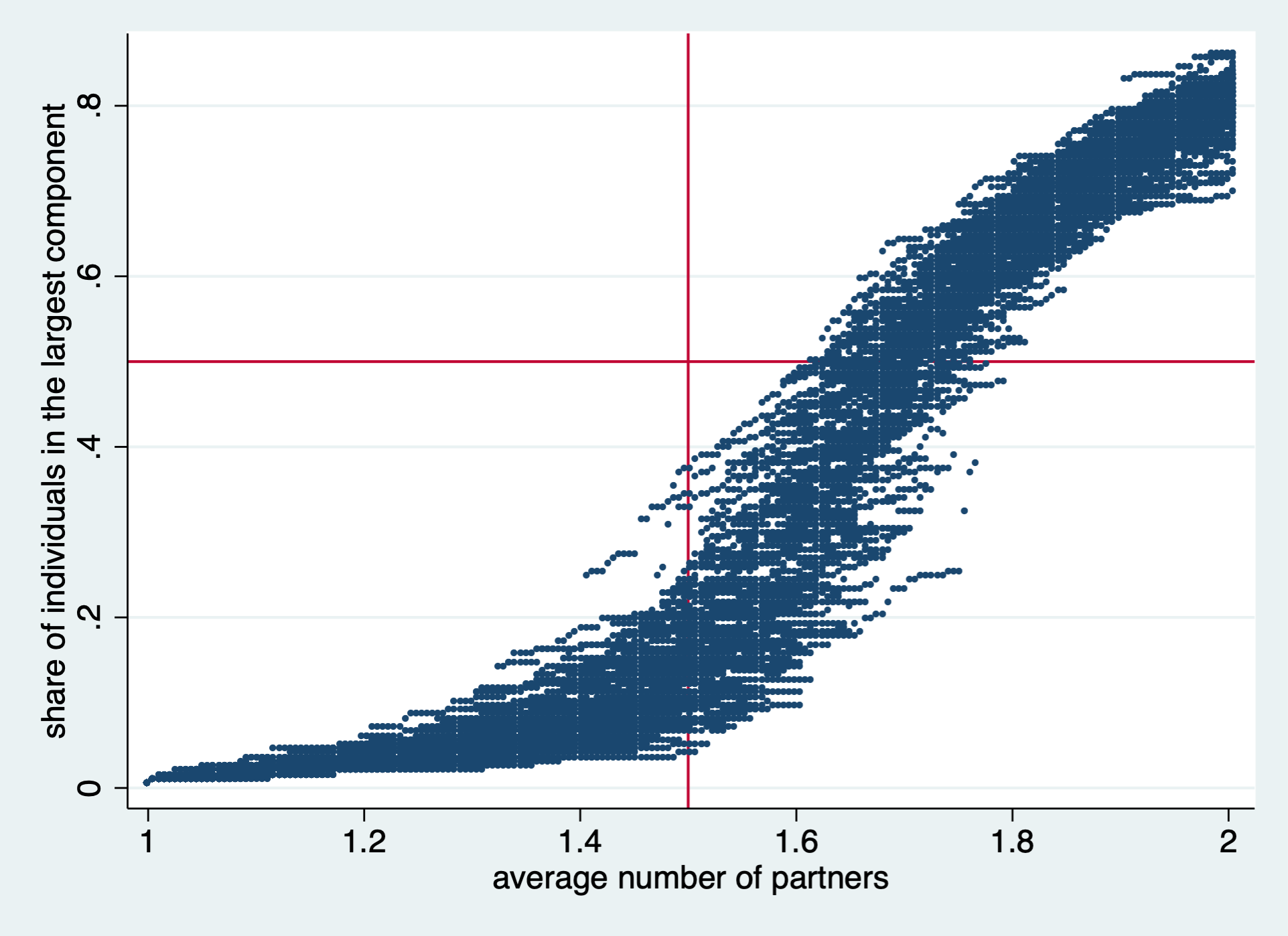
I have created a simple NetLogo model to illustrate the mechanics of my reasoning. You are welcome to play with it yourself. Starting from a population of 200 couples (and ignoring gender), and running it 100 times, I obtain the familiar phase transition, with the share of individuals in the largest component rising rapidly after the average number of partners per person crosses the 1.5 threshold. The vertical red line in the figure shows the threshold; the horizontal one is drawn at 0.5. Above that line, the majority of individuals are in the “one love” giant component. Notice also that, when the average number of partners reaches 2, about 80% of all polyamorists are part of the giant component.

Phase transition in size of the giant component as the average number of partners crosses the 1.5 line

Obtaining data

Now the question is: do polyamorous people actually have over 1.5 relationships on average? Like so many empirical questions, this one looks simple, but it is not. To answer it, you first have to define what “a relationship” is. Humans entertain a bewildering array of relationships, each one of which can imply, or not, romance (and how do you even define that?), sex, living together, parenting together, sharing finances and so on. They differ by duration, time spent together per week or per year, and so on. Coming up with a meaningful definition is not easy.

Supposing you do hammer out a definition, then you have to get yourself some serious data. Again, this is difficult. To quote the authors of the 2012 Loving More survey:

Truly randomized surveys […] are difficult, if not impossible, to obtain among hidden populations.

And, sure enough, I have been unable to find solid data about the average number of partners in polyamorous individuals.

The Loving More survey itself, for all its limitations, is one of the richest sources of empirical data on human behavior in polyamory: it involved over 4,000 Americans who self-identify as polyamorous. But the question “how many relationships do you have” was not asked. We do know that respondents reported an average of 4 sexual partners in the year previous to the survey. The exact same question is also asked in the (statistically legit) General Social Survey: there, a random sample of the U.S. population reported 3.5 sexual partners on average during the year previous to the survey. The difference is statistically significant, but it is not large, and anyway it only refers to recent sexual partners. Frankly, I have no idea how to infer values for the average number of romantic relationships from these numbers.

So, there is a significant empirical challenge here. But, if you solve it, you get to write the missing paper on polyamory, with the exciting conclusion that the “one love global network” exists, or not. I am looking forward to reading it!

Photo credit: unknown author from this site (Google says it’s labelled for reuse)

Do you speak networks?

Leave a reply

The more I use the Internet, the more I grow fascinated with networks, because they behave in unexpected, counterintuitive ways. They seem to summon order from chaos as if by magic. Consider the web: large masses of amateurs who don’t know each other and have no command structure should produce some kind of shapeless informational blob, right? Wrong. Day after day, people and content inexorably self-organize in such a way that they are one or few clicks away from each other. Building an exhaustive map of the Internet is impossible, but finding any one thing in it is quite easy. It is a bit like sticking your hand in the proverbial haystack and finding a needle, every time.

The more I study networks and the more they amaze me for their ability to organize information, in an apparently effortless way. Reading the history of scientific exploration of social networks is almost dizzying. Stanley Milgram gives random American letters for other random Americans asking the former to deliver through an unroken chain of aquaintances, and a surprising number of them reaches home in very few steps. Mark Granovetter discovers that aquaintances are more effective than close friends or family in finding us jobs. Fredrik Liljeros looks at a network of sexual contacts, and concludes that the existence of a small number of very promiscuous people renders AIDS impossible to eliminate. Nathan Eagle finds that the prosperity of a small area can be predicted from the pattern of allocation of calling time across their contacts of that area’s inhabitants (in poorer communities people spend a higher share of their calling time with one or two contacts). All these results seem independent of the actual people in the networks: in almost all models nodes are identical. All the action is in the link structure. Network papers are academic, but somewhat alien: Hogwarts comes to mind.

I am convinced that the properties of networks can help explain many phenomena that we experience every day but don’t really understand – and give us anxiety. Why do we feel surrounded by young, successful entrepreneurs (though there’s not that many of them)? Why were peer-to-peer file sharing services fatal to the recorded music industry? How does Wikipedia work so well?

My Holy Grail is to tame online social networks, forging them in a powerful, precise tool to design and deliver public policies. I have done it before in Visioni Urbane e Kublai, but a lot of time I had to steer by instinct. I was lucky, but for this to become a generalised method I need to understand it a lot better. So I study the language of networks: these days I am often at the European University Institute in Florence, to attend Fernando Vega-Redondo’s Complex Social Networks course. It’s a bit tough (I get up at 5 a.m., because Fernando usually lectures at 8.45 sharp), but so be it. I really need to understand this thing.

Do you speak networks? (Italiano)

4 Replies

Più uso Internet, più mi affascinano le reti, perché si comportano in modo inaspettato, controintuitivo. L’ordine sembra emergervi dal caos in modo quasi magico. Considerate il web: grandi masse di persone che non si conoscono, prive di strutture di comando e di professionalità nel produrre e gestire informazione, dovrebbero dare luogo a una specie di blob, no? E invece, infallibilmente, persone e contenuti finiscono per autorganizzarsi in modo da essere a pochi clicks (spesso uno solo) le une agli altri. Costruire una mappa esaustiva di Internet è impossibile, ma trovarvi qualcosa è abbastanza facile. È come mettere una mano nel proverbiale pagliaio e tirarne fuori un ago al primo tentativo, tutte le volte che cerchiamo un ago.

Più studio le reti e più mi sorprendono per la loro capacità di organizzare l’informazione, apparentemente senza nessuno sforzo. Leggere la storia dell’esplorazione scientifica delle reti sociali dà quasi le vertigini. Stanley Milgram affida a cittadini americani scelti a caso lettere per altri cittadini americani, sempre scelti a caso, e un numero sorprendente di esse arriva a destinazione in pochi passaggi (i famosi sei gradi di separazione). Mark Granovetter scopre che i conoscenti casuali sono più efficaci degli amici intimi e dei familiari nel trovarci lavoro . Fredrik Liljeros studia le reti di rapporti sessuali e conclude che un piccolo numero di persone molto promiscue impedirà la scomparsa dell’AIDS. Nathan Eagle predice la prosperità delle comunità locali a partire da come i suoi abitanti dividono il tempo che passano al telefono (gli abitanti delle comunità più povere passano una quota alta del proprio tempo di chiamata con una o poche persone). Tutti questi risultati sembrano indipendenti dalle persone che compongono le reti: in quasi tutti i modelli i nodi sono identici tra loro. L’unica cosa che li distingue – e che genera le proprietà straordinarie dei modelli – è la struttura dei links. Roba che sembra uscita da un corso di laurea, sì, ma di Hogwarts.

Mi sono convinto che le proprietà delle reti possano contribuire a spiegare molti fenomeni di cui facciamo esperienza quotidiana, ma che non capiamo – e che spesso ci danno ansia. Perché abbiamo la sensazione di essere circondati da imprenditori di successo brillanti e creativi (sebbene numericamente queste persone non siano poi tante)? Perché il file sharing in peer-to-peer ha messo alle corde l’industria musicale? Perché Wikipedia funziona così bene?

Il mio Sacro Graal è di domare le reti sociali online, forgiandole in uno strumento potente e preciso per progettare e attuare le politiche pubbliche. L’ho già fatto con Visioni Urbane e Kublai, ma ho dovuto fare molte scelte sulla base del mio istinto. È andata bene, ma perché questo diventi un metodo generalizzabile ho bisogno di capirne molto, molto di più. E quindi studio la lingua delle reti: in questo periodo vado spesso all’European University Institute di Firenze per frequentare il corso di Complex Social Networks di Fernando Vega-Redondo. È un po’ dura (mi alzo alle cinque del mattino, perché Fernando fa quasi sempre lezione alle 8.45 precise), ma pazienza. Io questa cosa la devo assolutamente capire.